What Is The Solution Of Log2 (3x + 7) = 3? Unravel The Mystery Behind This Math Equation
**Alright, let's dive straight into it. If you're here, chances are you're scratching your head wondering, "What is the solution of log2 (3x + 7) = 3?" Don't worry, you're not alone. This logarithmic equation might seem intimidating at first, but trust me, it’s not as scary as it looks. In this article, we'll break it down step by step so you can solve it like a pro. So, buckle up, and let’s unravel the secrets behind this math problem together.
Logarithms can be a bit tricky for some folks, but they're actually one of the most fascinating parts of mathematics. They're like the secret codes of numbers, and once you crack them, you’ll feel like a mathematical wizard. If you’ve ever wondered how to solve equations like log2 (3x + 7) = 3, you're in the right place. We’ll guide you through the process with simple explanations and real-life examples.
Before we dive deeper, let’s quickly set the stage. This article isn’t just about solving one equation; it’s about equipping you with the tools and knowledge to tackle similar problems in the future. Whether you're a student trying to ace your math exam or someone brushing up on their skills, this guide is tailored for you. Now, let’s get started!
- What Is Food Analog Definition A Deep Dive Into The World Of Food Analog
- What Is The Simple Definition Of Food Analog A Bitesized Guide
Understanding Logarithms: The Basics
First things first, what exactly are logarithms? Think of them as the opposite of exponents. While exponents tell you how many times you multiply a number by itself, logarithms tell you how many times you need to multiply a base number to reach a specific value. For example, in log2 (3x + 7) = 3, the base is 2, and the equation is asking, "To what power must 2 be raised to equal (3x + 7)?"
Here’s a quick breakdown:
- Logarithm = Opposite of exponentiation
- Base = The number you're raising to a power
- Argument = The number you're trying to reach
In this case, the base is 2, and the argument is (3x + 7). The solution lies in figuring out the value of x that satisfies the equation. Easy, right? Well, let’s keep going to make it even clearer.
- Barack Obama Iq Unveiling The Brilliance Behind The Leadership
- James Franco Height A Closer Look At The Actors Stats And Career
Breaking Down log2 (3x + 7) = 3
Now that we’ve got the basics down, let’s focus on the equation itself. The goal here is to isolate x. To do that, we’ll follow a series of logical steps:
Step 1: Rewrite the logarithmic equation in its exponential form. Remember, logarithms and exponents are like two sides of the same coin. So, log2 (3x + 7) = 3 can be rewritten as:
2³ = 3x + 7
Step 2: Simplify the equation. Since 2³ equals 8, the equation becomes:
8 = 3x + 7
Step 3: Solve for x. Subtract 7 from both sides:
8 - 7 = 3x
1 = 3x
Finally, divide both sides by 3:
x = 1/3
Voila! The solution to the equation log2 (3x + 7) = 3 is x = 1/3. Not so bad, was it?
Why Logarithms Matter in Real Life
Now that we’ve solved the equation, let’s talk about why logarithms are so important. You might be thinking, "When will I ever use this in real life?" The truth is, logarithms pop up in more places than you’d expect. Here are a few examples:
- Sound Engineering: Decibels, the unit used to measure sound intensity, are based on logarithms. Without logarithms, sound engineers wouldn’t be able to accurately adjust volume levels.
- Earthquake Measurement: The Richter scale, which measures the magnitude of earthquakes, is logarithmic. This means a magnitude 6 earthquake is 10 times stronger than a magnitude 5 earthquake.
- Finance: Compound interest calculations often involve logarithmic functions. If you’re planning your financial future, understanding logarithms can help you make smarter investment decisions.
So, whether you're designing a sound system, studying natural disasters, or growing your savings, logarithms are your secret weapon.
Common Mistakes When Solving Logarithmic Equations
Even the best of us make mistakes sometimes, especially when dealing with complex equations. Here are a few common pitfalls to watch out for:
- Forgetting to check the domain: Not all logarithmic equations have real solutions. Always ensure the argument (the number inside the logarithm) is positive.
- Misinterpreting the base: The base of the logarithm is crucial. Double-check that you’re using the correct base when solving the equation.
- Skipping steps: Taking shortcuts might seem tempting, but it often leads to errors. Break the problem into manageable steps and solve it systematically.
By being aware of these mistakes, you can avoid them and solve logarithmic equations with confidence.
Tips for Mastering Logarithmic Equations
Want to become a logarithmic wizard? Here are some tips to help you master these equations:
- Practice, practice, practice: The more problems you solve, the better you’ll get. Try working through a variety of logarithmic equations to build your skills.
- Use online resources: There are tons of free resources available online, including video tutorials and practice problems. Take advantage of them to deepen your understanding.
- Ask for help: If you’re stuck, don’t hesitate to ask a teacher, tutor, or classmate for assistance. Sometimes, a fresh perspective can make all the difference.
Remember, mastering logarithms takes time and effort, but with persistence, you’ll get there.
Advanced Applications of Logarithms
For those of you who want to take things to the next level, here are some advanced applications of logarithms:
Logarithmic Differentiation
Logarithmic differentiation is a powerful technique used in calculus to simplify complex functions. By taking the natural logarithm of both sides of an equation, you can transform products into sums and powers into products, making differentiation much easier.
Logarithmic Scales
Logarithmic scales are used in various fields, from astronomy to economics. They allow us to represent large ranges of values in a compact and manageable way. For example, the pH scale, which measures acidity and basicity, is logarithmic.
Logarithmic Growth
Logarithmic growth occurs when the rate of change of a quantity decreases over time. This type of growth is common in biology, economics, and technology. Understanding logarithmic growth can help you make predictions and analyze trends more effectively.
Tools for Solving Logarithmic Equations
In today’s digital age, there are plenty of tools available to help you solve logarithmic equations. Here are a few worth checking out:
- Graphing Calculators: Tools like the TI-84 or Desmos can graph logarithmic functions and solve equations step by step.
- Math Apps: Apps like Photomath and WolframAlpha can solve logarithmic equations and provide detailed explanations.
- Online Tutorials: YouTube is full of excellent tutorials on logarithms. Find a channel that resonates with you and follow along.
These tools can save you time and help you verify your solutions, but don’t rely on them too heavily. Building your own problem-solving skills is key to long-term success.
Real-Life Examples of log2 (3x + 7) = 3
Let’s bring this equation to life with a real-world example. Imagine you’re a computer programmer working on a data compression algorithm. You need to determine the optimal value of x that satisfies the equation log2 (3x + 7) = 3. By solving this equation, you can optimize the algorithm and improve its efficiency.
Or, picture yourself as a scientist analyzing population growth. You’re studying a species whose population doubles every three years. By using logarithms, you can predict the population size at any given time and make informed decisions about conservation efforts.
See? Logarithms aren’t just abstract concepts; they have practical applications in the real world.
Conclusion: Take Action and Keep Learning
In conclusion, solving the equation log2 (3x + 7) = 3 is just the beginning of your logarithmic journey. By understanding the basics, avoiding common mistakes, and exploring advanced applications, you can unlock the full potential of logarithms. Remember, practice makes perfect, so keep challenging yourself with new problems.
Now, it’s your turn. Leave a comment below and let us know what you think. Did you find this guide helpful? What other math topics would you like to learn about? And don’t forget to share this article with your friends and family. Together, we can make math fun and accessible for everyone!
Daftar Isi
- Understanding Logarithms: The Basics
- Breaking Down log2 (3x + 7) = 3
- Why Logarithms Matter in Real Life
- Common Mistakes When Solving Logarithmic Equations
- Tips for Mastering Logarithmic Equations
- Advanced Applications of Logarithms
- Tools for Solving Logarithmic Equations
- Real-Life Examples of log2 (3x + 7) = 3
- Conclusion: Take Action and Keep Learning
- Daftar Isi
- The Boring Magazine Com Your Ultimate Source For Thoughtprovoking Reads
- Three Blind Mice Shrek A Tale Beyond The Fairy Tale
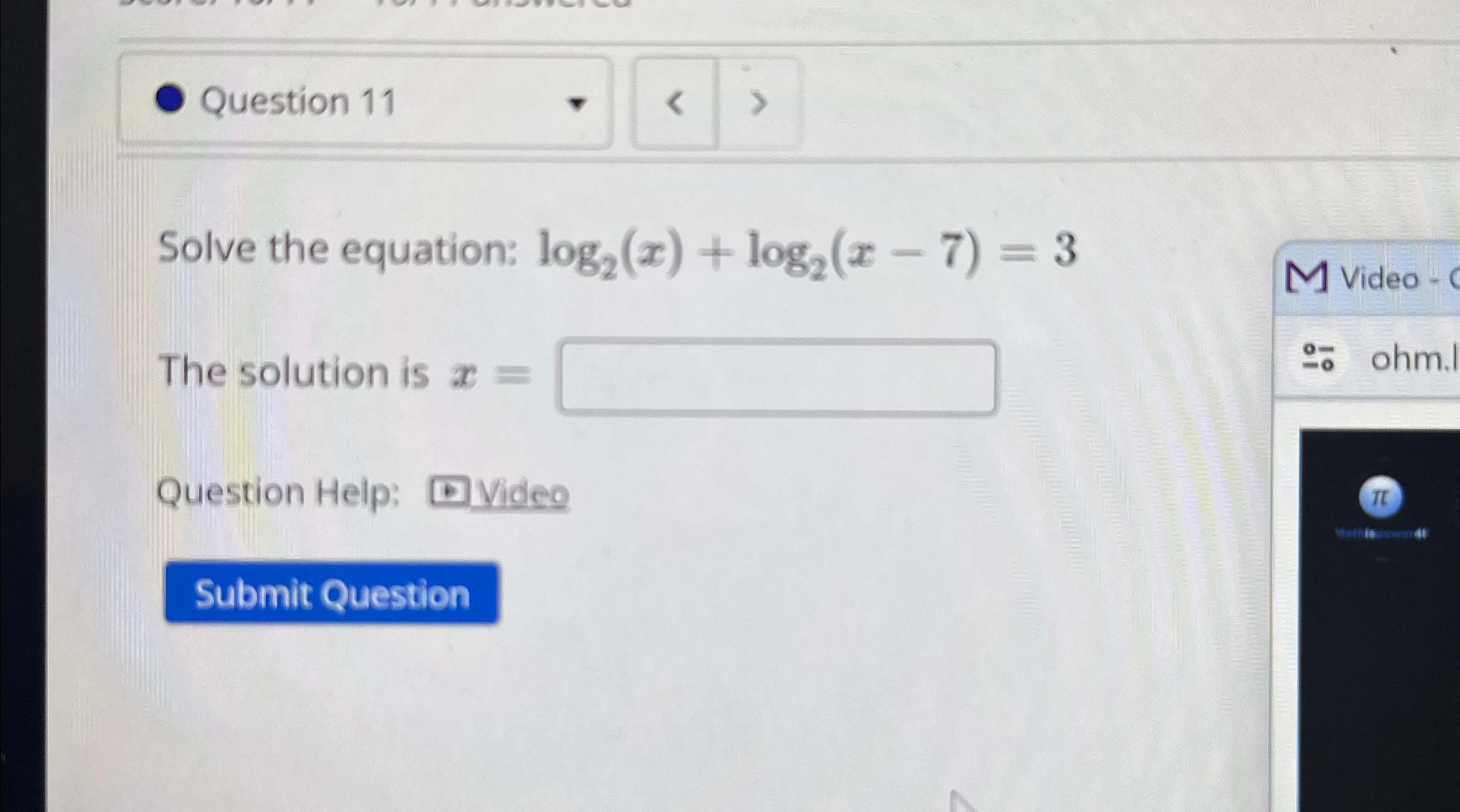
Solved Solve the equation log2(x)+log2(x7)=3The solution

Give the exact solution set of \log (3 x+2)+\log (x1)1 \g Quizlet
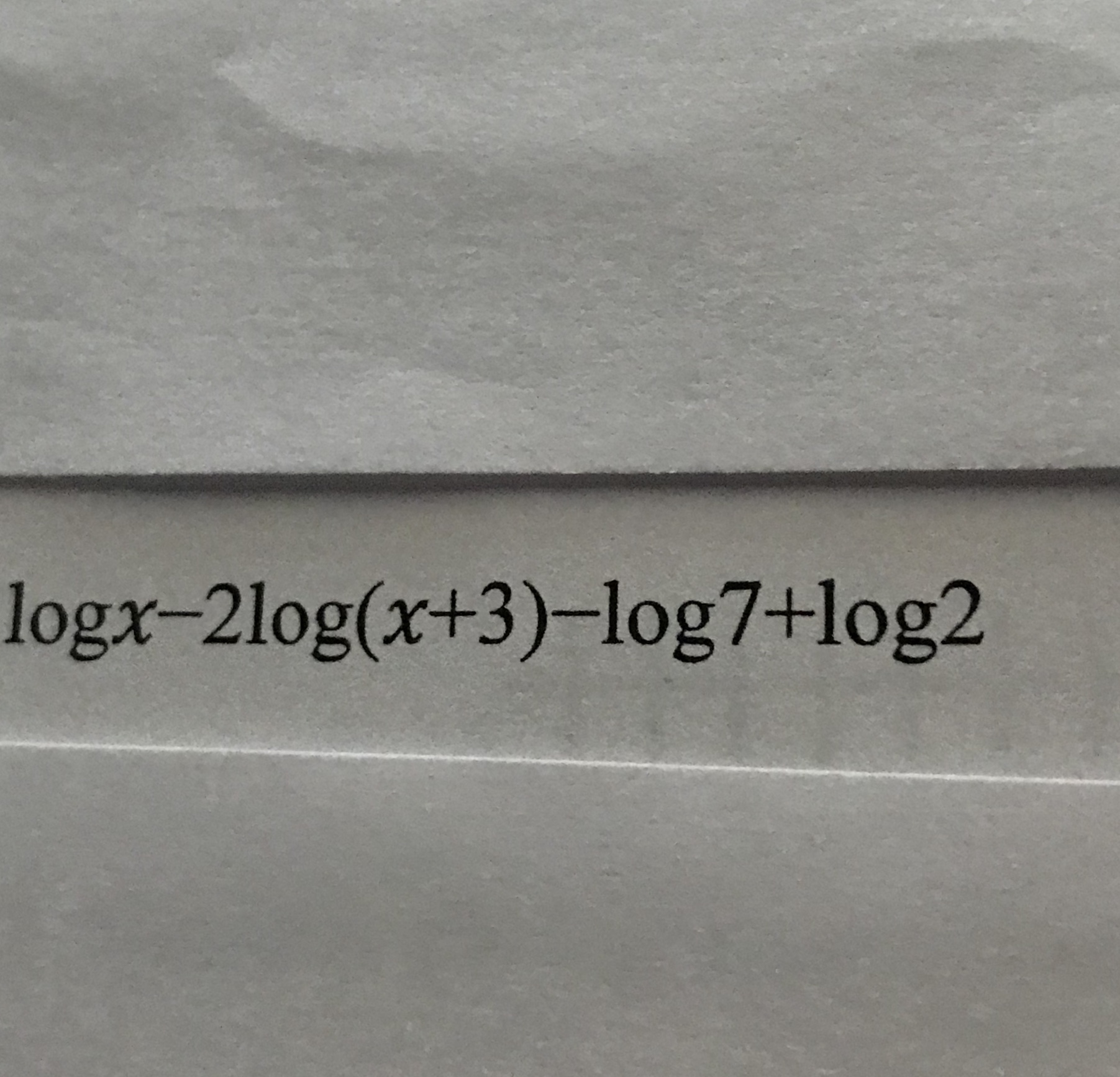
Answered logx2log(x+3)log7+log2 bartleby